Геометрическая загадка: как найти сторону треугольника, зная радиус описанной окружности

Как найти сторону треугольника, зная радиус описанной окружности?

В этой статье мы отправимся в увлекательное путешествие по миру геометрии и разберемся с интересным вопросом: можно ли определить сторону треугольника, если известен радиус его описанной окружности? Этот вопрос может показаться загадкой, но, вооружившись математическими инструментами, мы найдем решение и раскроем секреты этой геометрической задачи.

Связь между радиусом окружности и треугольником

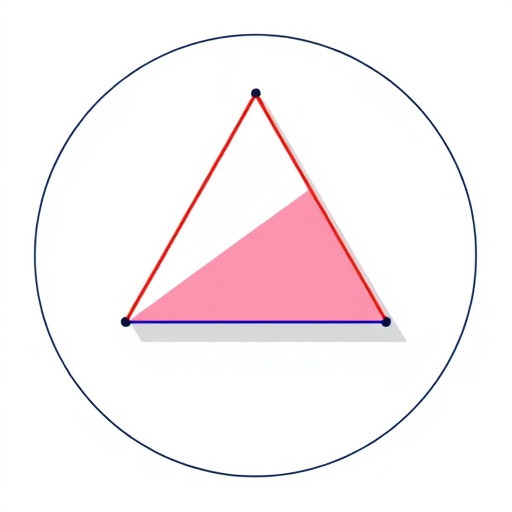
Начнем с того, что описанная окружность треугольника - это окружность, проходящая через все его вершины. Радиус такой окружности тесно связан с треугольником и содержит важную информацию о его свойствах. Представьте, что радиус окружности - это ключ, который может открыть дверь к тайнам треугольника. Наша задача - найти этот ключ и использовать его правильно.

Когда мы говорим о радиусе описанной окружности, мы подразумеваем расстояние от центра окружности до любой из вершин треугольника. Это расстояние одинаково для всех вершин, и именно оно является ключевым параметром в нашей задаче.

Формула для нахождения стороны треугольника

Теперь перейдем к сути вопроса: как же найти сторону треугольника, зная радиус описанной окружности? Оказывается, существует специальная формула, которая устанавливает связь между радиусом (R) и длиной стороны (a) в треугольнике. Эта формула - настоящий помощник в решении нашей задачи.

Формула имеет следующий вид:

a = 2R * sin(A/2)

Где:

• a - длина стороны треугольника, которую мы хотим найти;
• R - радиус описанной окружности;
• A - мера одного из углов треугольника.

Эта формула - как волшебная палочка, которая позволяет нам раскрыть тайну неизвестной стороны. Но как она работает?

Разбор формулы и пример

Давайте разберемся в каждом элементе формулы. Множитель 2 в формуле указывает на то, что мы работаем с радиусом окружности, а не диаметром. Функция синуса (sin) связана с углами треугольника. Угол A, который используется в формуле, может быть любым углом треугольника.

Представьте, что мы строим треугольник на лугу, а радиус окружности - это длина веревки. Мы привязываем веревку к колу в центре луга, а другой конец держим в руке. Если мы хотим найти длину стороны треугольника, то должны измерить расстояние от центра (радиус) и знать меру одного из углов.

Рассмотрим пример. Допустим, у нас есть треугольник с радиусом описанной окружности R = 5 см, и мы хотим найти длину стороны, соответствующей углу A = 60 градусов. Подставляя значения в формулу:

a = 2 * 5 см * sin(60 градусов / 2) = 10 см * sin(30 градусов) ≈ 10 см * 0.5 = 5 см

Таким образом, длина стороны треугольника равна 5 см.

Практическое применение

Этот метод нахождения стороны треугольника имеет множество практических применений. Например, в архитектуре и строительстве, когда необходимо рассчитать длину балки или диагонали здания, зная радиус описанной окружности и углы треугольника.

Также, данный подход может быть полезен в навигации и картографии. Воображая землю как сферу, мы можем использовать радиус окружности как масштаб, а углы для определения расстояний между точками.

Заключение

В этой статье мы раскрыли секреты нахождения стороны треугольника, зная радиус описанной окружности. Формула, связывающая радиус и сторону, является мощным инструментом в решении геометрических задач. Теперь вы знаете, как найти ключ к тайнам треугольника и использовать его в различных практических ситуациях.

Таким образом, ответ на вопрос "Как найти сторону треугольника, зная радиус окружности?" - это применение специальной формулы, учитывающей радиус и углы треугольника. Геометрия, как и вся математика, предоставляет нам инструменты для решения самых разных задач, даже если на первый взгляд они кажутся неразрешимыми.

# F.A.Q.

Как найти сторону треугольника, зная радиус описанной окружности?

Для решения этой задачи можно использовать формулу, связывающую стороны треугольника и радиус описанной окружности. Если известна одна сторона треугольника, а также радиус описанной окружности, можно найти другие стороны. Формула: - Для стороны a: **a = √(4R² - b² - c²)** - Для стороны b: **b = √(4R² - a² - c²)** - Для стороны c: **c = √(4R² - a² - b²)** Где: - **a, b, c** - стороны треугольника; - **R** - радиус описанной окружности. Замените известные значения в формулу и найдите значение неизвестной стороны.

Можно ли найти все стороны треугольника, зная только радиус окружности?

Нет, одной информации о радиусе описанной окружности недостаточно для определения всех сторон треугольника. Вам также необходимы данные хотя бы об одной стороне или других элементах треугольника (например, углах).

Какие еще формулы связаны с радиусом описанной окружности?

Существует несколько формул, связывающих стороны и радиус описанной окружности: - Формула для нахождения периметра треугольника: **P = a b c = 4R** - Формула для площади треугольника: **S = √[3(a b c)(a b-c)(a-b c)(-a b c)] = √[3(4R)(4R-2a)(4R-2b)(4R-2c)]** - Формула для радиуса вписанной окружности: **r = √[(a b-c)(a-b c)/2(a b c)]** Где: - **P** - периметр; - **S** - площадь; - **r** - радиус вписанной окружности.

Как найти радиус описанной окружности, если известны стороны треугольника?

Для нахождения радиуса описанной окружности, когда известны все стороны, используйте формулу: **R = a²bc / √[(a b c)(a b-c)(a-b c)]**

Применима ли эта формула для всех видов треугольников?

Да, эти формулы применимы для любых видов треугольников: равносторонних, равнобедренных и прямоугольных.

Где можно применить эти знания на практике?

Знание этих формул может быть полезно при решении геометрических задач, в архитектуре и инженерных расчётах, а также в различных прикладных задачах, связанных с треугольниками и окружностями.