Как найти катеты в прямоугольном треугольнике

В этом руководстве мы рассмотрим простой метод нахождения катетов в прямоугольном треугольнике, используя теорему Пифагора.

Оглавление

• Введение
• Теорема Пифагора
• Нахождение катетов
• Пример

Введение

Прямоугольный треугольник - это особый вид треугольника, у которого один из углов равен 90 градусам. Такие треугольники имеют множество применений в геометрии и тригонометрии. В этой статье мы сосредоточимся на поиске катетов, которые являются сторонами, примыкающими к углу в 90 градусов.

Теорема Пифагора

Теорема Пифагора - это фундаментальное утверждение в геометрии, которое устанавливает связь между сторонами прямоугольного треугольника. Согласно теореме, квадрат длины гипотенузы (стороны противолежащей углу в 90 градусов) равен сумме квадратов длин двух катетов. Математически это можно выразить следующим образом:

Гипотенуза² = Катет₁² Катет₂²

Нахождение катетов

Чтобы найти длину катетов, мы можем использовать теорему Пифагора. Если известны длины двух сторон прямоугольного треугольника, мы можем найти длину третьей стороны, а затем использовать эту информацию для определения катетов.

Предположим, мы знаем длину гипотенузы (c) и одного катета (a). Мы можем найти длину второго катета (b) следующим образом:

b = √(c² - a²)

Обратите внимание, что мы используем квадратный корень, чтобы получить положительное значение для длины катета.

Пример

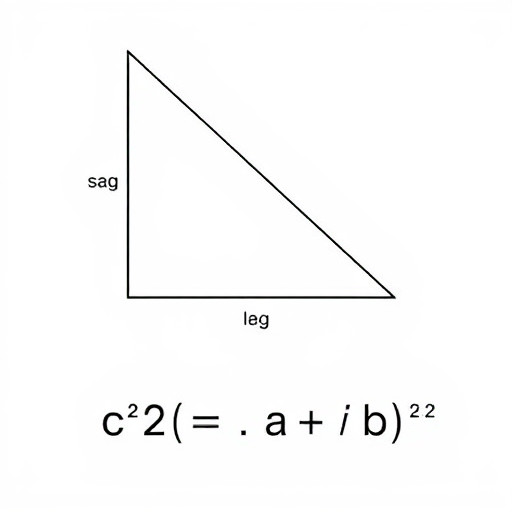
Рассмотрим прямоугольный треугольник, у которого длина гипотенузы равна 5 единицам, а длина одного катета равна 3 единицам. Мы можем найти длину второго катета:

b = √(5² - 3²) = √(25 - 9) = √16 = 4

Таким образом, длина второго катета равна 4 единицам.

Как найти катеты прямоугольного треугольника, зная его гипотенузу и угол?

Если у вас есть длина гипотенузы и мера одного из острых углов, вы можете найти катеты, используя тригонометрические функции. Например, если известен угол α, то катеты можно вычислить по формулам: - Катет противолежащий углу α: a = c * cos(α) - Катет прилежащий к углу α: b = c * sin(α) Где c - длина гипотенузы.

Можно ли найти катеты, зная только длину гипотенузы?

Нет, для определения катетов в прямоугольном треугольнике недостаточно знать только длину гипотенузы. Необходимо также знать хотя бы один из острых углов или длину одного из катетов.

Как найти катеты, если известен один катет и угол между ним и гипотенузой?

В этом случае вы можете использовать теорему синусов. Если известен катет a и угол α между ним и гипотенузой, то другой катет b можно найти по формуле: b = (a * sin(α)) / sin(90° - α) Где sin - синус, а 90° - мера прямого угла.

Что делать, если известны оба катета, но нужно найти гипотенузу?

Если известны оба катета прямоугольного треугольника, вы можете найти длину гипотенузы по теореме Пифагора: Гипотенуза (c) = √(a² b²) Где a и b - длины катетов.

Есть ли простые способы запомнить эти формулы?

Да, есть несколько мнемонических правил, которые могут помочь запомнить формулы. Например: - "СОС" - для формулы катета противолежащего углу: "Синус Отвесной Стороны". - "СИС" - для формулы катета прилежащего к углу: "Синус Измеренного Стороны". - "Пифагор" - для теоремы Пифагора: "Приложил Ухо К Пифагору, Он Решил".

Эти F.A.Q. охватывают различные ситуации, с которыми вы можете столкнуться при поиске катетов в прямоугольном треугольнике. Помните, что тригонометрические функции и теорема Пифагора являются мощными инструментами в решении таких задач.