Объем прямоугольного параллелепипеда: пошаговое руководство для 5 класса

Как найти объем прямоугольного параллелепипеда: пошаговое руководство для 5 класса

В 5 классе учащихся знакомят с основами геометрии, и одним из важных понятий, которое они изучают, является объем фигур. Прямоугольный параллелепипед - это простая геометрическая фигура, которая помогает детям освоить принципы измерения объема. В этой статье мы подробно рассмотрим, как найти объем прямоугольного параллелепипеда, используя наглядные примеры и пошаговое руководство.

## Что такое прямоугольный параллелепипед?

Прямоугольный параллелепипед - это трехмерная фигура, которая имеет шесть прямоугольных граней. Представьте себе коробку для обуви или кирпич - это и есть примеры прямоугольных параллелепипедов. Все грани у такой фигуры прямые, а углы равны 90 градусам. Параллелепипед имеет длину, ширину и высоту, и именно эти параметры помогут нам в расчете объема.

## Почему важно знать объем фигур?

Изучение объема фигур имеет практическое значение в повседневной жизни. Например, когда вы идете в магазин и хотите купить упаковку сока, знание объема поможет вам понять, сколько жидкости вы приобретаете. Или, если вы планируете перевезти вещи в новую квартиру, расчет объема коробок позволит оптимально организовать пространство. Таким образом, умение находить объем прямоугольного параллелепипеда - это не только школьная задача, но и полезный навык в реальной жизни.

## Как найти объем прямоугольного параллелепипеда: пошаговая инструкция

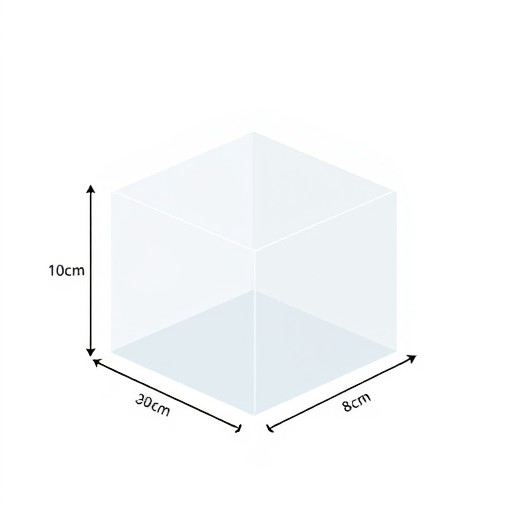
1. **Измерьте стороны.** Первым шагом является измерение длин трех сторон параллелепипеда. Допустим, у нас есть коробка с длиной 10 см, шириной 5 см и высотой 8 см. Эти измерения являются ключевыми для наших расчетов.

2. **Понятие формулы объема.** Объем прямоугольного параллелепипеда рассчитывается по формуле: Объем = длина × ширина × высота. Эта формула отражает принцип заполнения пространства внутри фигуры. Представьте, что вы наполняете коробку кубиками, и количество кубиков будет равно объему.

3. **Подставьте значения.** Теперь подставьте измеренные значения в формулу. В нашем примере: Объем = 10 см × 5 см × 8 см.

4. **Выполните вычисления.** Последовательно выполните умножение: 10 × 5 = 50, а затем 50 × 8 = 400. Таким образом, объем нашей коробки равен 400 кубическим сантиметрам (куб. см)

5. **Анализ результата.** Полученный результат показывает, что внутри коробки можно разместить 400 маленьких кубиков со стороной 1 см. Это наглядно демонстрирует объем нашего параллелепипеда.

## Примеры из реальной жизни

- **Упаковка продуктов:** Когда вы видите на упаковке молока или сока указание объема, например, 1 литр, это означает, что внутри находится жидкость, занимающая пространство в 1000 кубических сантиметров.

- **Строительство:** При возведении зданий архитекторы и строители используют расчеты объемов для определения количества материалов. Например, для заливки фундамента важно знать объем бетона, который потребуется.

- **Перевозка грузов:** Компании, занимающиеся транспортировкой, используют измерения объема для оптимизации загрузки грузовиков и контейнеров. Это позволяет эффективно использовать пространство и снизить расходы.

## Заключение

Находя объем прямоугольного параллелепипеда, вы не только решаете школьные задачи, но и развиваете навыки, которые пригодятся в будущем. Этот процесс помогает понять связь между измерениями и пространством, а также применять математику в практических ситуациях. Помните, что формула объема - это мощный инструмент, который открывает двери в мир трехмерных фигур и их секретов.

Как найти объем прямоугольного параллелепипеда в 5 классе?

Для нахождения объема прямоугольного параллелепипеда необходимо умножить длину, ширину и высоту фигуры. Обозначим длину как a, ширину как b, а высоту как h. Тогда формула объема будет иметь вид: V = a * b * h. Например, если у вас есть прямоугольный параллелепипед с длиной 5 см, шириной 3 см и высотой 2 см, то объем можно найти так: V = 5 см * 3 см * 2 см = 30 кубических сантиметров (куб. см) или 30 см³.

Что такое прямоугольный параллелепипед и его элементы?

Прямоугольный параллелепипед — это трехмерная фигура, у которой все углы прямые, а все грани — прямоугольники. Элементами прямоугольного параллелепипеда являются:

• Длина — расстояние между двумя противоположными гранями, которые параллельны.
• Ширина — расстояние между двумя другими противоположными гранями, также параллельными.
• Высота — расстояние между верхней и нижней основаниями параллелепипеда.

Почему для объема умножают длину, ширину и высоту?

Объем прямоугольного параллелепипеда представляет собой пространство, занимаемое фигурой. Чтобы найти это пространство, мы должны умножить размеры фигуры в трех измерениях: длину, ширину и высоту. Умножение этих элементов дает нам объем, который измеряется в кубических единицах (например, кубических сантиметрах или кубических метрах).

Как измерить длину, ширину и высоту параллелепипеда на практике?

Чтобы измерить эти элементы, вам потребуются линейка или рулетка:

1. Измерьте длину параллелепипеда, проведя линейку вдоль одной из длинных сторон и записав значение.
2. Измерьте ширину, проведя линейку вдоль одной из сторон, перпендикулярной длине, и запишите результат.
3. Для измерения высоты поставьте параллелепипед на одно из оснований и измерьте расстояние от основания до верхней точки.

Можно ли найти объем, зная только две измерения?

Нет, для нахождения объема прямоугольного параллелепипеда необходимо знать все три измерения: длину, ширину и высоту. Если у вас есть только два измерения, вы можете рассчитать площадь основания (длина * ширина), но не объем.

Какие единицы измерения используются для объема?

Объем обычно измеряется в кубических единицах, таких как кубические сантиметры (куб. см или см³), кубические метры (куб. м или м³) или литры (л). Выбираемая единица зависит от размера фигуры. Например, для небольших предметов, таких как коробка конфет, используют кубические сантиметры, а для больших объектов, таких как комната, — кубические метры.

Эти F.A.Q. должны помочь учащимся 5 класса понять основные принципы расчета объема прямоугольного параллелепипеда и ответить на распространенные вопросы по этой теме.